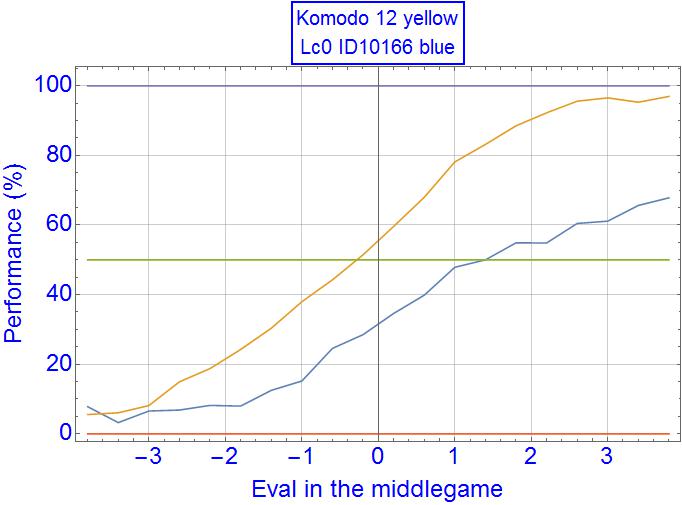
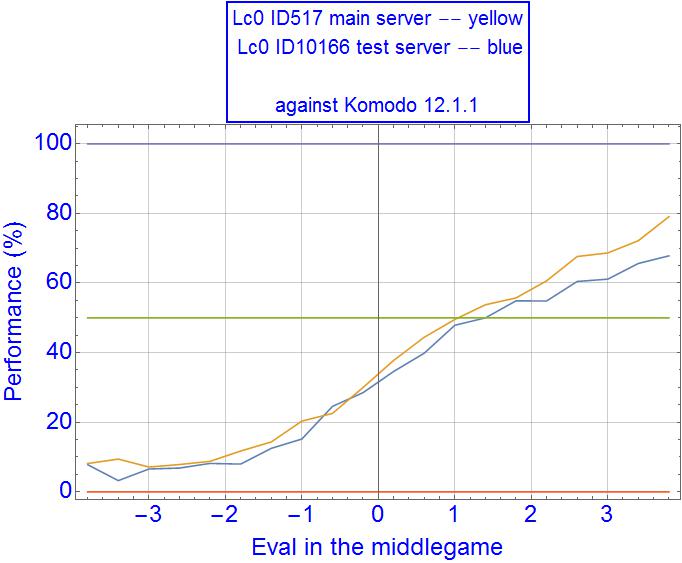
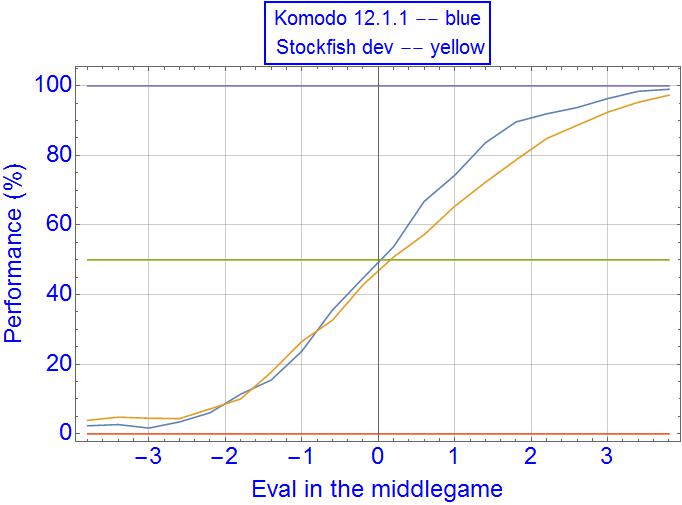
I maybe should specify the conditions, as the plots depend (mildly) on them. The time control was short, 0.1s/move for Lc0 ID10166, 0.013s/move for Komodo 12.1.1 (I tuned Komodo's time control to such a small value to equal it in strength to Lc0). In these conditions Lc0 had about 150-200 nodes per move, a pretty low number.
Code: Select all
players, min, max, Gcnt, Wcnt, Lcnt, Dcnt, perf(%),
K1211, -4.00, -3.60, 207, 5, 189, 13, 5.56,
K1211, -3.60, -3.20, 330, 10, 300, 20, 6.06,
K1211, -3.20, -2.80, 406, 25, 365, 16, 8.13,
K1211, -2.80, -2.40, 548, 56, 440, 52, 14.96,
K1211, -2.40, -2.00, 714, 78, 524, 112, 18.77,
K1211, -2.00, -1.60, 934, 129, 610, 195, 24.25,
K1211, -1.60, -1.20, 1352, 243, 774, 335, 30.36,
K1211, -1.20, -0.80, 1659, 413, 812, 434, 37.97,
K1211, -0.80, -0.40, 2223, 680, 935, 608, 44.26,
K1211, -0.40, 0.00, 2993, 1101, 1014, 878, 51.45,
K1211, 0.00, 0.40, 2965, 1350, 780, 835, 59.61,
K1211, 0.40, 0.80, 1605, 929, 352, 324, 67.98,
K1211, 0.80, 1.20, 858, 597, 114, 147, 78.15,
K1211, 1.20, 1.60, 505, 391, 56, 58, 83.17,
K1211, 1.60, 2.00, 383, 325, 30, 28, 88.51,
K1211, 2.00, 2.40, 284, 257, 17, 10, 92.25,
K1211, 2.40, 2.80, 204, 193, 7, 4, 95.59,
K1211, 2.80, 3.20, 174, 167, 5, 2, 96.55,
K1211, 3.20, 3.60, 149, 138, 3, 8, 95.30,
K1211, 3.60, 4.00, 132, 125, 1, 6, 96.97,
lc0_v16, -4.00, -3.60, 96, 6, 87, 3, 7.81,
lc0_v16, -3.60, -3.20, 93, 1, 88, 4, 3.23,
lc0_v16, -3.20, -2.80, 99, 5, 91, 3, 6.57,
lc0_v16, -2.80, -2.40, 124, 3, 110, 11, 6.85,
lc0_v16, -2.40, -2.00, 159, 9, 142, 8, 8.18,
lc0_v16, -2.00, -1.60, 244, 9, 214, 21, 7.99,
lc0_v16, -1.60, -1.20, 336, 23, 275, 38, 12.50,
lc0_v16, -1.20, -0.80, 428, 29, 327, 72, 15.19,
lc0_v16, -0.80, -0.40, 566, 80, 368, 118, 24.56,
lc0_v16, -0.40, 0.00, 1019, 148, 586, 285, 28.51,
lc0_v16, 0.00, 0.40, 1571, 316, 800, 455, 34.60,
lc0_v16, 0.40, 0.80, 1606, 444, 770, 392, 39.85,
lc0_v16, 0.80, 1.20, 1482, 526, 589, 367, 47.87,
lc0_v16, 1.20, 1.60, 1306, 475, 475, 356, 50.00,
lc0_v16, 1.60, 2.00, 1046, 436, 334, 276, 54.88,
lc0_v16, 2.00, 2.40, 918, 382, 293, 243, 54.85,
lc0_v16, 2.40, 2.80, 798, 379, 212, 207, 60.46,
lc0_v16, 2.80, 3.20, 661, 335, 188, 138, 61.12,
lc0_v16, 3.20, 3.60, 566, 301, 124, 141, 65.64,
lc0_v16, 3.60, 4.00, 505, 273, 93, 139, 67.82,
(min, max) refer to eval window for the designated engine.
Gcnt is the total number of occurrences in games this eval window for that engine occurred in the match.
perf (%) is the averaged performance of the designated engine inside that (min, max) eval interval, or (Wcnt + Dcnt/2) / Gcnt.
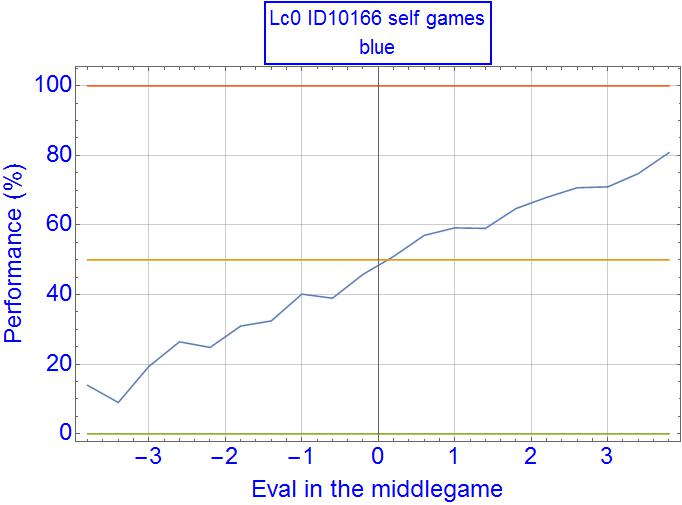
In self-games the plot is pretty symmetric, although not completely. The raw data is here:
Code: Select all
players, min, max, Gcnt, Wcnt, Lcnt, Dcnt, perf(%),
lc0_v16, -4.00, -3.60, 61, 6, 50, 5, 13.93,
lc0_v16, -3.60, -3.20, 61, 4, 54, 3, 9.02,
lc0_v16, -3.20, -2.80, 80, 10, 59, 11, 19.38,
lc0_v16, -2.80, -2.40, 121, 19, 76, 26, 26.45,
lc0_v16, -2.40, -2.00, 159, 20, 100, 39, 24.84,
lc0_v16, -2.00, -1.60, 234, 43, 132, 59, 30.98,
lc0_v16, -1.60, -1.20, 325, 62, 176, 87, 32.46,
lc0_v16, -1.20, -0.80, 493, 134, 231, 128, 40.16,
lc0_v16, -0.80, -0.40, 762, 208, 376, 178, 38.98,
lc0_v16, -0.40, 0.00, 1153, 382, 478, 293, 45.84,
lc0_v16, 0.00, 0.40, 1428, 547, 519, 362, 50.98,
lc0_v16, 0.40, 0.80, 1195, 524, 356, 315, 57.03,
lc0_v16, 0.80, 1.20, 750, 349, 211, 190, 59.20,
lc0_v16, 1.20, 1.60, 542, 243, 145, 154, 59.04,
lc0_v16, 1.60, 2.00, 366, 182, 74, 110, 64.75,
lc0_v16, 2.00, 2.40, 312, 164, 52, 96, 67.95,
lc0_v16, 2.40, 2.80, 251, 145, 41, 65, 70.72,
lc0_v16, 2.80, 3.20, 174, 107, 34, 33, 70.98,
lc0_v16, 3.20, 3.60, 135, 85, 18, 32, 74.81,
lc0_v16, 3.60, 4.00, 99, 69, 8, 22, 80.81,
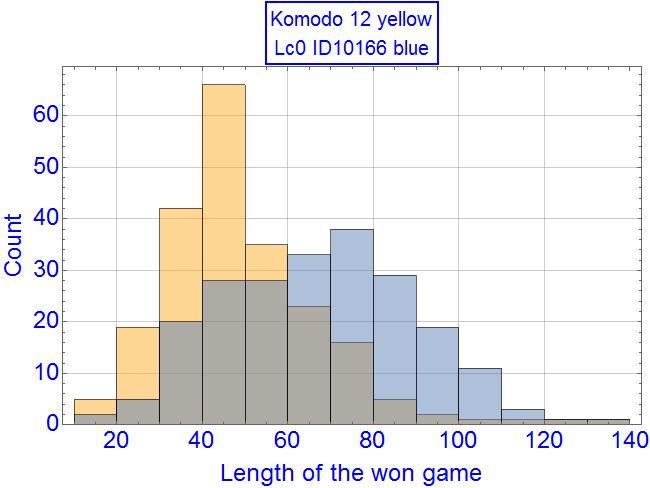
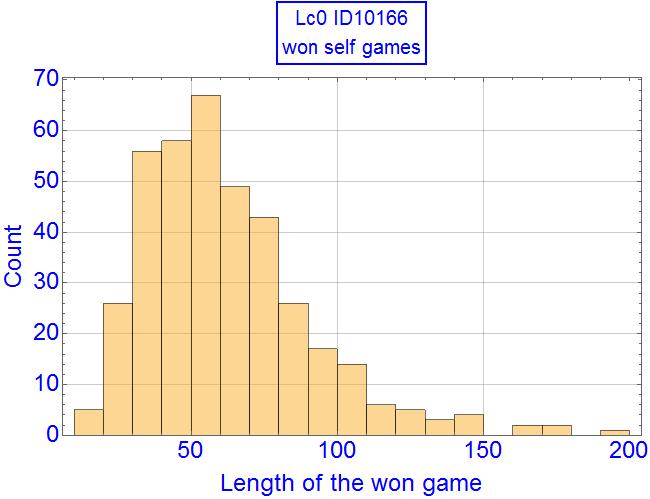
Now the won self-games of Lc0 has the median of 55.5 moves, below the median length of Lc0 wins against equal in strength Komodo (67), and above the median length of won games of Komodo (46). No adjudication was used.