What about SF with a big time handicap?(let say slow it down by a factor of 100)Laskos wrote: ↑Wed Jan 23, 2019 1:00 pm"A" is important in schizophrenia, but ELO1 - ELO2 is even more important in defining the degree of illness.Michel wrote: ↑Tue Jan 22, 2019 1:22 pm Nice! Lots of ideas!
So a fully schizophrenic Leela is just two players. The score of a regular engine against a fully schizophrenic Leela with given elo1,elo2 would be the same as its score against two regular players with elo1 and elo2 respectively.
A partially schizophrenic Leela is more complicated. It is like two players but one of them gets to play more than the other.
Maybe on the lines like "positional, tactical" (as test-suites show) one can improvise a plausible explanation of this schizophrenia.
On these lines, one can imagine two sorts of distributions of outcomes in many games:
An accumulation of many very small errors/advantages (limited variance), mostly positional advantages in the case of Leela, which leads to Gaussian statistics through the central limit theorem, well mimicked in CDF by a logistic. Very high ELO1 for Leela in a pool of regular engines might derive from this.
Some errors may have a Cauchy or Levy-like distributions (not defined or infinite variance) and we have the "Levy flight", where the total distance traveled (to the outcome of a game) is almost always dominated by the largest single or at most two errors. Here Leela "excels" in frequency of these sort of errors compared to strong regular engines, hence deriving its low ELO2.
Both lead in many games to CDF well approximated by logistics, but two different logistics. Regular engines are close enough in properties to assimilate both these properties into one single Elo logistic in ratings among them, so that an individual regular engine in a pool of other regular engines might be schizophrenic with ELO1 - ELO2 of say about small 50 Elo, 100 Elo even 200 Elo points. Lets's call this very mild schizophrenia "moody", and regular engine can be at most moody in a pool of regular engines. Their rating will be well described by A*ELO1 + (1-A)*ELO2, and with these rating it will obey the general Elo model. But Leela is so different that ELO1 - ELO2 is above 1000 Elo points (the fit gave 1070), and it cannot fit a logistic Elo model in a pool of regular engines by this simple weighted averaging, it is truly pathologically schizophrenic. I will plot the cases of moody regular engine (at most 200 points between ELO1 and ELO2) and schizophrenic Leela-like engine (1000 points between ELO1 and ELO2), at full "split-personality" (A=0.5):
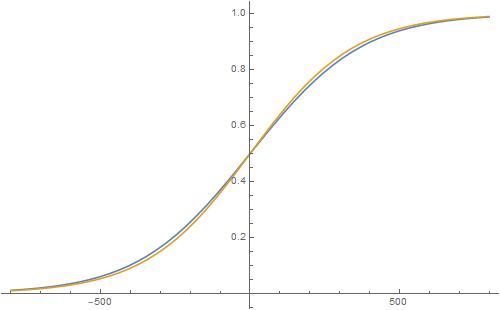
Moody regular engine (ELO1 = 100, ELO2 = -100, A=0.5):
The blue line is the true sum of the two logistics separated by 200 Elo points. The brown line is a logistic with average (ELO1 + ELO2)/2 = 0. This moody regular engine still fits very well with a logistic given by average rating.
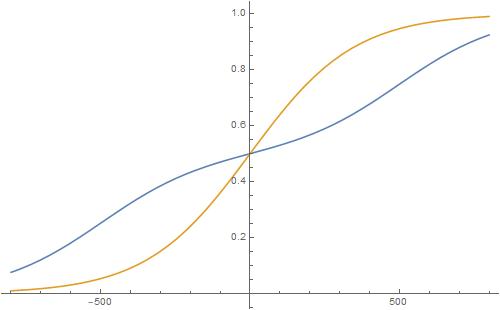
Schizophrenic Leela-like engine (ELO1 = 500, ELO2 = -500, A=0.5):
The blue line is the true sum of the two logistics separated by 1000 Elo points. The brown line is a logistic with average (ELO1 + ELO2)/2 = 0. Now we see that 1000+ Elo points difference makes a huge difference, the average logistic fit fails badly, and the true sum gives indeed compressed ratings, only explainable by ELO1, ELO2, A separately, and not averaging.
This sort of explanation, aside test-suites, where we see highly pathological positional/tactical behavior of Leela can be seen from comparing evals, and we also can see that regular engines probably never diverge by 200+ Elo points in their moodiness, as the rule of thumb for regular engines is that they are getting stronger positionally and tactically fairly hand in hand.
From an easy experiment, we can probably derive that compared to the simplest eval --- material + PST. even a top SF10 eval cannot get 1000 Elo points difference against a regular engine:
depth=1
Score of SF10 vs Predateur 2.1: 980 - 4 - 16 [0.988] 1000
Elo difference: 766.23 +/- 86.73
Finished match
In Predateur 2.1 even PST are somehow dubious.
But the search of Predateur is similarly weaker, by about the same Elo value. So, they will not look pathological in rating lists one to another, at most moody.
OTOH, Leela is by some 500 Elo points stronger than SF10 in eval, SF10 at depth 1 (about 20-30 nodes searched) and Leela at nodes=20, and 350 Elo points stronger even at nodes=1 than SF10 depth=1. And tactically, LC0 is like a weak regular engine, and 1000+ Elo points full blown pathology in ELO1 - ELO2 can be explained.
It would be interesting to have a basic eval with SF search, or viceversa, SF eval with basic search, to see if they exhibit rating pathology. Almost surely not to the degree Leela exhibits.
Are we going to find a similiar behaviour to leela?