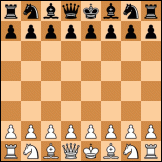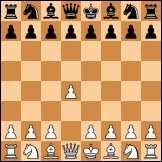
Yes that is correct. The number 5.8e41 is the number of symmetry equivalent ways to put all the 32 initial pieces on the board, so no legality and pawns not on 1st or 8th row etc. It is indeed 1/8 of your factorial computation.Ajedrecista wrote: Then your number is 1/8 of this second attempt. Same question again: what I am doing wrong?
In the first version, you were doing a 4! incorrect. That would only apply if the 2 kings and queens were identical pieces. Instead, you need to do (1!)^4. This gives a factor of 24, and then another factor of 1/8 gives you my number.
Here's my Mathematica code, doing the calculation in 3 different ways. First as a specific coefficient in a cycle index polynomial, then as a Multinomial function, and finally as a bunch of factorials.
Code: Select all
In[56]:= Z[x1_,x2_,x4_]:=(1*x1^64+2*x1^8 x2^28 + 3*x2^32+2*x4^16)/8
In[57]:= ChessZ =Z[(P0+P1+P2+P3+P4+P5+P6+P7+P8+ P9 +P10 +P11 + P12 ),(P0^2+P1^2+P2^2+P3^2+P4^2+P5^2+P6^2+P7^2+P8^2+P9^2+P10^2+P11^2+P12^2),(P0^4+P1^4+P2^4+P3^4+P4^4+P5^4+P6^4+P7^4+P8^4+P9^4+P10^4+P11^4+P12^4)]
Out[57]= 1/8 ((P0+P1+P10+P11+P12+P2+P3+P4+P5+P6+P7+P8+P9)^64+2 (P0+P1+P10+P11+P12+P2+P3+P4+P5+P6+P7+P8+P9)^8 (P0^2+P1^2+P10^2+P11^2+P12^2+P2^2+P3^2+P4^2+P5^2+P6^2+P7^2+P8^2+P9^2)^28+3 (P0^2+P1^2+P10^2+P11^2+P12^2+P2^2+P3^2+P4^2+P5^2+P6^2+P7^2+P8^2+P9^2)^32+2 (P0^4+P1^4+P10^4+P11^4+P12^4+P2^4+P3^4+P4^4+P5^4+P6^4+P7^4+P8^4+P9^4)^16)
In[58]:= Coefficient[ChessZ,P0^62P1 P2 ]
Coefficient[ChessZ,P0^58 P1 P2 P3^2 P4^2 ]
Coefficient[ChessZ,P0^32 P1 P2 P3 P4 P5^2 P6^2 P7^2 P8^2 P9^2 P10^2 P11^8 P12^8 ]
Out[58]= 518
Out[59]= 1686946884
Out[60]= 579340836948476205149027870013146842320000
In[67]:= Multinomial[32,8,8,2,2,2,2,2,2,1,1,1,1]/8
Out[67]= 579340836948476205149005747790410708800000
In[66]:= (64!/(32! (8!)^2 (2!)^6))/8
Out[66]= 579340836948476205149005747790410708800000