The S in SCRelu is "squared" so you do you mean squared but not clipped?
Devlog of Leorik
Moderator: Ras
-
lithander

- Posts: 915
- Joined: Sun Dec 27, 2020 2:40 am
- Location: Bremen, Germany
- Full name: Thomas Jahn
Re: Devlog of Leorik
-
op12no2
- Posts: 553
- Joined: Tue Feb 04, 2014 12:25 pm
- Location: Gower, Wales
- Full name: Colin Jenkins
Re: Devlog of Leorik
Yeah, sorry I was using the bullet naming convention; squared but not clipped.
https://github.com/op12no2/lozza/blob/c ... a.js#L1994
https://github.com/op12no2/lozza/blob/c ... a.js#L1994
-
lithander

- Posts: 915
- Joined: Sun Dec 27, 2020 2:40 am
- Location: Bremen, Germany
- Full name: Thomas Jahn
Re: Devlog of Leorik
When I tried Squared-Clipped-Relu vs Clipped-Relu I couldn't get it to gain at first because I didn't know how to implement it without losing too much speed. Only when I figured out how I could continue to use _mm256_madd_epi16 instead of widening to int too early the SCRelu managed to beat CRelu in practice.
So I'm using quantization which means instead of using floats (32bit) values are represented with integer values. Everything is multiplied with a quantization factor (e.g. 255) and then rounded to nearest int. So if you have float values in the range [0..1] and chose a quantization factor 255 now all these values neatly fit into 8bits. (with a loss of precision ofc)
When doing NNUE inference normally you'd compute the activation function and then multiply the result with weight. For SCRelu you do this:
With quantization however it's more efficient to do it like this:
And this is only because the clamped a is known to be in the range of [0..255] and if you quantize the weights to be in the range of [-127..127] then voila the result doesn't overflow a short and you can use _mm256_madd_epi16 for twice the throughput than what you'd get if you'd really square the clipped activation.

...in other words. This is complicated stuff not because the math is hard but you also need to run these billions of multiply & add operations as fast as possible or the small precision gain from a slightly superior activation function isn't worth the speedloss.
So, in my case I think SqrRelu won't help me improve because I can't see a way to implement it as fast as quantized SCRelu currently is implemented. I need the clipping & and quantization to squeeze everything into shorts!
So I'm using quantization which means instead of using floats (32bit) values are represented with integer values. Everything is multiplied with a quantization factor (e.g. 255) and then rounded to nearest int. So if you have float values in the range [0..1] and chose a quantization factor 255 now all these values neatly fit into 8bits. (with a loss of precision ofc)
When doing NNUE inference normally you'd compute the activation function and then multiply the result with weight. For SCRelu you do this:
Code: Select all
f(x) = clamp(x, 0, 1)^2 * weightWith quantization however it's more efficient to do it like this:
Code: Select all
a = clamp(x, 0, 1)
f(x) = (a * weight) * a
And this is only because the clamped a is known to be in the range of [0..255] and if you quantize the weights to be in the range of [-127..127] then voila the result doesn't overflow a short and you can use _mm256_madd_epi16 for twice the throughput than what you'd get if you'd really square the clipped activation.
...in other words. This is complicated stuff not because the math is hard but you also need to run these billions of multiply & add operations as fast as possible or the small precision gain from a slightly superior activation function isn't worth the speedloss.
So, in my case I think SqrRelu won't help me improve because I can't see a way to implement it as fast as quantized SCRelu currently is implemented. I need the clipping & and quantization to squeeze everything into shorts!
-
op12no2
- Posts: 553
- Joined: Tue Feb 04, 2014 12:25 pm
- Location: Gower, Wales
- Full name: Colin Jenkins
Re: Devlog of Leorik
I only have a single perspective layer and use an int32 for acculumating the eval itself and Javascript has no native SIMD facilities so my life is a lot easier in this respect  I think Stormphrax has SqrRelu in a recent net - presumably on the final layer based on what you have said (?).
I think Stormphrax has SqrRelu in a recent net - presumably on the final layer based on what you have said (?).
-
lithander

- Posts: 915
- Joined: Sun Dec 27, 2020 2:40 am
- Location: Bremen, Germany
- Full name: Thomas Jahn
*New* Release of version 3.1
I just uploaded version 3.1 binaries to github: https://github.com/lithander/Leorik/releases/tag/3.1
Version 3.1 improves Leorik's NNUE evaluation by using a larger network (640 HL neurons) and adopting SCReLU activation. The network was trained from scratch over 19 generations. The network 640HL-S-5288M-Tmix-Q5-v19 that releases with version 3.1, was trained on 5.2B positions from generation 13 to 19. Search improvements include the addition of Correction History, increased reduction of late quiet moves, a dynamic threshold for identifying such moves, and the introduction of RFP with dynamic margins derived from NMP statistics.
I haven't run matches against 3.0 or other engines yet so I'm pretty curious how big the strength increase is. Will post later about that.
Version 3.1 improves Leorik's NNUE evaluation by using a larger network (640 HL neurons) and adopting SCReLU activation. The network was trained from scratch over 19 generations. The network 640HL-S-5288M-Tmix-Q5-v19 that releases with version 3.1, was trained on 5.2B positions from generation 13 to 19. Search improvements include the addition of Correction History, increased reduction of late quiet moves, a dynamic threshold for identifying such moves, and the introduction of RFP with dynamic margins derived from NMP statistics.
I haven't run matches against 3.0 or other engines yet so I'm pretty curious how big the strength increase is. Will post later about that.
-
lithander

- Posts: 915
- Joined: Sun Dec 27, 2020 2:40 am
- Location: Bremen, Germany
- Full name: Thomas Jahn
*New* Release of version 3.1
Code: Select all
/cutechess-cli.exe -engine conf="Leorik-3.1" -engine conf="Leorik-3.0.1"
-each tc=5+0.1 -openings file="UHO_2024_8mvs_big_+095_+114.pgn"
-concurrency 11
Score of Leorik-3.1 vs Leorik-3.0.1: 2874 - 483 - 1643 [0.739] 5000
... Leorik-3.1 playing White: 1988 - 50 - 462 [0.888] 2500
... Leorik-3.1 playing Black: 886 - 433 - 1181 [0.591] 2500
... White vs Black: 2421 - 936 - 1643 [0.648] 5000
Elo difference: 180.9 +/- 8.3, LOS: 100.0 %, DrawRatio: 32.9 %-
lithander

- Posts: 915
- Joined: Sun Dec 27, 2020 2:40 am
- Location: Bremen, Germany
- Full name: Thomas Jahn
Re: Devlog of Leorik
The preliminary results of testing of Leorik 3.1 for the CEGT 40/4 list confirm my previous estimate of +180 Elo, now against a wider range of opponents!
Meanwhile I have updated the Leorik binaries released on github to version 3.1.2 of similar strength but where the internal eval is scaled by a factor before getting printed in the uci output. Outputting the raw eval values makes the engine look very dramatic as scores are about 3x bigger than what you'd expect. That's because training a net is all about minimizing the prediction error and not at all aware of what a centipawn is.
Only after release of 3.1 I learned that most engines scale the internal eval before printing and also how to derive a good scaling factor, namely with the tool: https://github.com/official-stockfish/WDL_model
You can give it a bunch of pgn files containing games that your engine has played and calculate the stats for your engine like this:Then run
100 is only correct, if you had no scaling before! (otherwise set according to your scaling factor)
...and within seconds you're presented with a scientific looking visualization
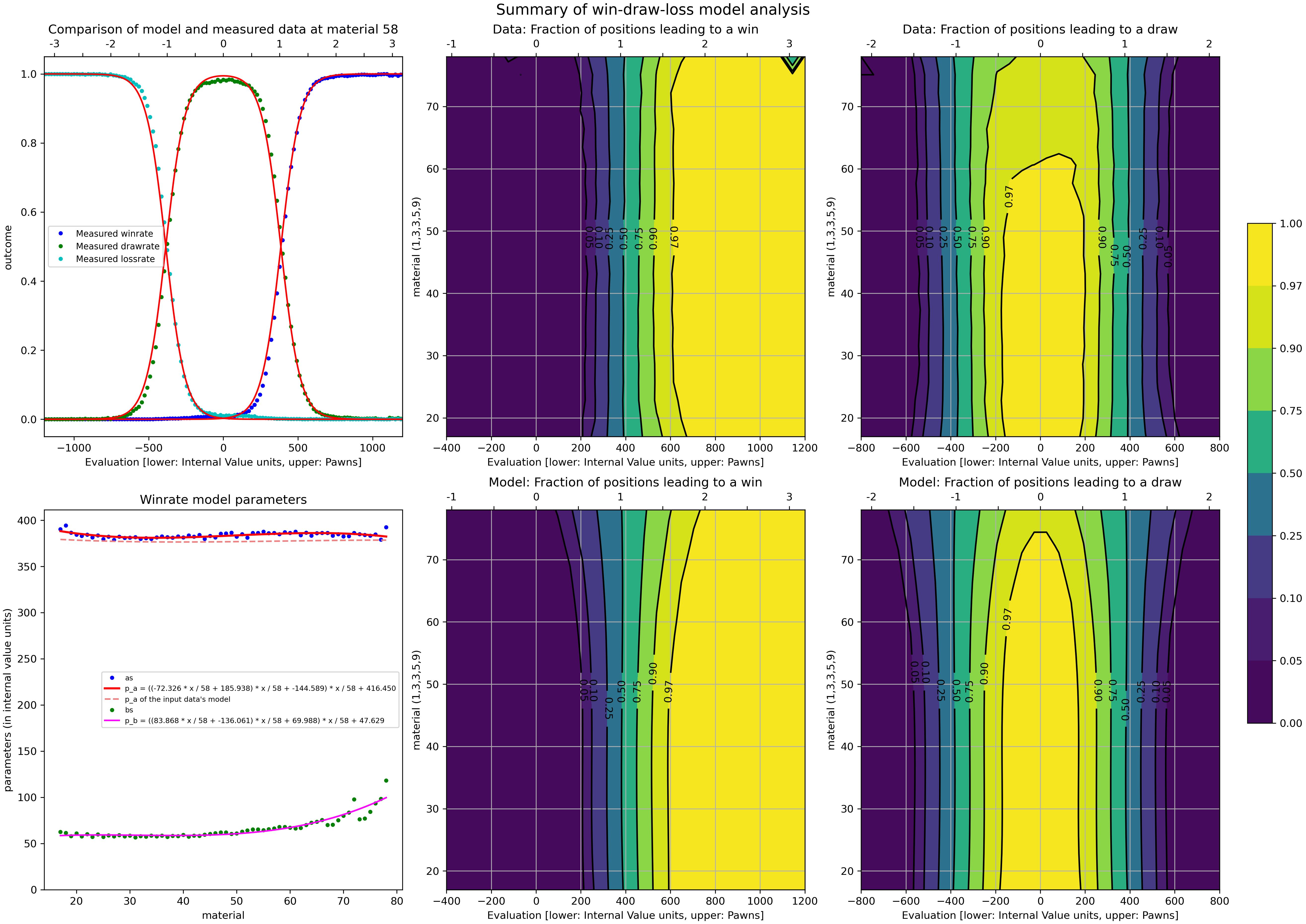
...and in the log you'll find a line like const int NormalizeToPawnValue = 306; and while I think it's a bit confusingly named it's the score at which the propability of a win/loss is 50% which is (according to stockfish) when you should evaluate the position as +/- 100 cp!
Meanwhile I have updated the Leorik binaries released on github to version 3.1.2 of similar strength but where the internal eval is scaled by a factor before getting printed in the uci output. Outputting the raw eval values makes the engine look very dramatic as scores are about 3x bigger than what you'd expect. That's because training a net is all about minimizing the prediction error and not at all aware of what a centipawn is.
Only after release of 3.1 I learned that most engines scale the internal eval before printing and also how to derive a good scaling factor, namely with the tool: https://github.com/official-stockfish/WDL_model
You can give it a bunch of pgn files containing games that your engine has played and calculate the stats for your engine like this:
Code: Select all
./scoreWDLstat.exe --matchEngine "Leorik-3.1"
Code: Select all
python .\scoreWDL.py --NormalizeToPawnValue 100...and within seconds you're presented with a scientific looking visualization

...and in the log you'll find a line like const int NormalizeToPawnValue = 306; and while I think it's a bit confusingly named it's the score at which the propability of a win/loss is 50% which is (according to stockfish) when you should evaluate the position as +/- 100 cp!
-
lithander

- Posts: 915
- Joined: Sun Dec 27, 2020 2:40 am
- Location: Bremen, Germany
- Full name: Thomas Jahn
Re: Devlog of Leorik
I have trained a number of networks all compatible with Leorik 3.1 binaries. You can download them from github here
Just make sure to place the nnue file you want besides the Leorik binary. Start the binary and confirm from the console output that the nnue file you wanted was loaded correctly!
I have included a graph showing how more neurons improves the accuracy of the networks (y-axis, less loss is better) but also requires a longer training duration (x-axis, more epochs takes longer) and finally I have annotated the graphs with the relative Elo gain of doubling the HL size.
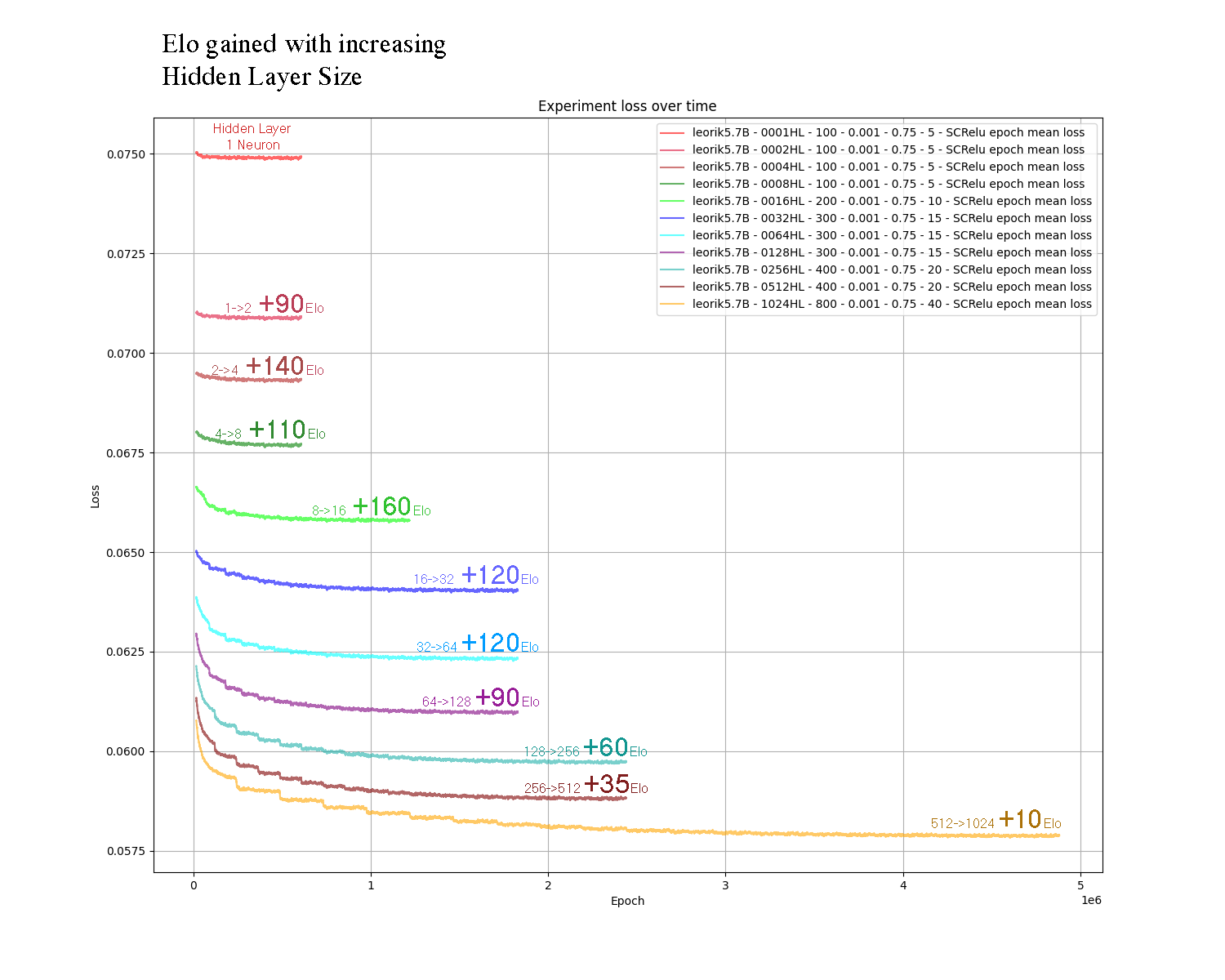
Just make sure to place the nnue file you want besides the Leorik binary. Start the binary and confirm from the console output that the nnue file you wanted was loaded correctly!
I have included a graph showing how more neurons improves the accuracy of the networks (y-axis, less loss is better) but also requires a longer training duration (x-axis, more epochs takes longer) and finally I have annotated the graphs with the relative Elo gain of doubling the HL size.
