Draw rate calculation between two elite players

[towforce]

What do you think of this formula construction

DrawRate = 1 / (1+exp(-(a-b*Rdiff+c*Ravg))

Swagging in some values for a, b, and c (I don't have time to do database mining at the moment). I used:
a=-10.69
b=0.005
c=0.000419

This gives a draw rate of 99.9% for two 4200 players, and a draw rate of 65% for two 2700 players. A draw rate of 58.2% for a 2800 vs 2700.
Obviously a, b, and c would need to be calibrated to available data for classical events and again for rapid events.

Very good!

[mbabigian]

Ajedrecista, again thanks for the reply and links. I'll check out the Swiss simulator when I get a chance.

I guess what bakes my noodle about Armageddon as a tie-breaker, is how do you simulate who got white when the entire tournament didn't even start. The unknowable part are the player's bids if, and when, they are tied and end up in Armageddon. If you can't anticipate who will receive white or just how steep the time odds are, it is difficult to give one player an arbitrary edge over the other. As players get better at bidding, you might think they will eventually bid no lower than what maintains there current Elo advantage. If they bid perfectly in this manner, the Elo advantage would be all that is needed to PRNG a winner for simulation purposes. You'd just end up with a binary result with the higher rated player taking the larger share of wins. Making assumptions about who will bid what, seems like a rabbit hole I'm likely to avoid. So when I get to the knockout format simulation, I'll likely just implement the Elo win% with no white advantage and return the result as win/lose and zero chance of draw. A poor, but programmable solution.

If however, two players are about to play Armageddon, you could simulate different bids by the players to determine who is likely to win based on time odds links you mentioned and rating difference. This to me would be a standalone program used to inform you on how low you can bid before your chances dip below 50/50. I'd be surprised if someone hasn't already attempted this as every top player should know the lower bound bid against a variety of opponents rated +- their own rating. That way if they end up needing to bid, they have a "no go" level in mind and bid accordingly.

Hopefully, I articulated that in a sensible way...

[mbabigian]

Very good!

Your reciprocal suggestion made it happen. The issues with the prior formulation did not occur to me until you mentioned them! Much appreciated.

[mbabigian]

Let me start by again saying thank you to Ajedrecista for the links he provided. Although I remember reading these discussions back in the day, I had completely forgot about them and the models they discussed. Although I looked at the draw rate formula for Davidson and Glen-Davidson, I could not get them to work properly. Perhaps I'm doing something wrong.

However, I have spent some time writing a program to find the coefficients for the Babigian Model (I figured I should name it ). I initially thought finding good coefficients would not be time consuming; however, I'll add that to the long list of things I was wrong about. After discovering the difficulty of finding the best/good values for three interacting coefficients, I rewrote my coefficient finder to be multi-threaded. That said, this is what I found:

Code: Select all

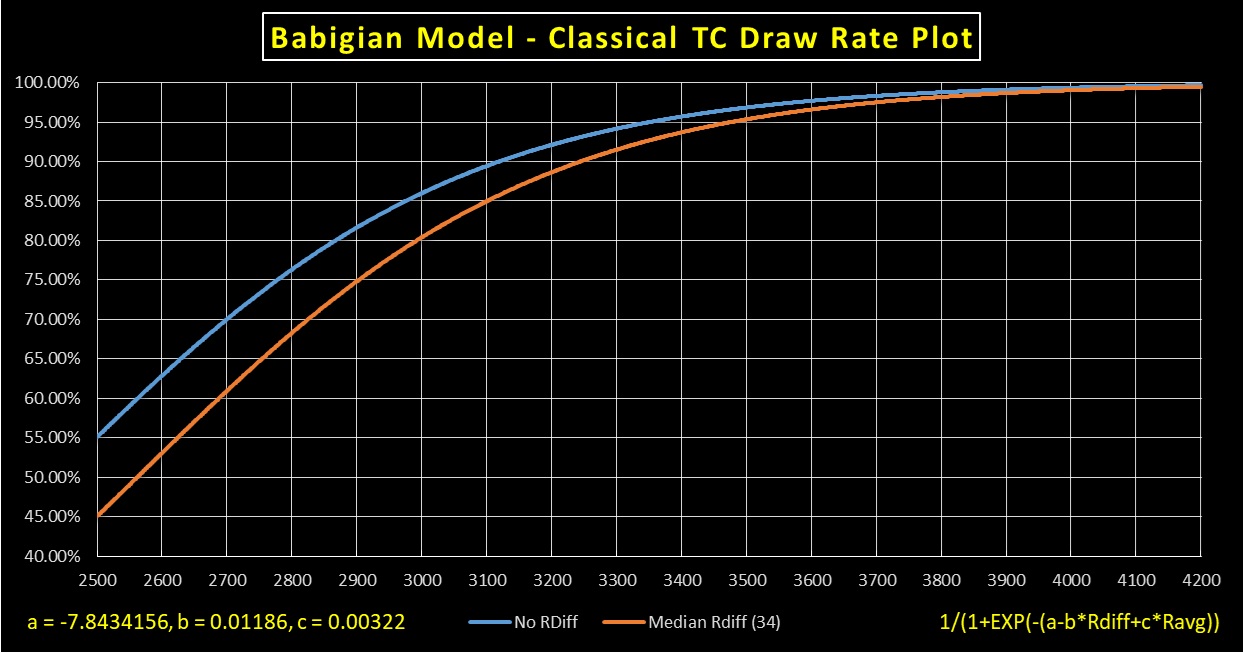
a=-7.8434156
b=0.01186
c=0.00322
DrawRate = 1 / (1+exp(-(a-b*Rdiff+c*Ravg))

I used the following data to model these values. software.farseer.org/Software/EliteChes ... 03-2023.7z The zip contains 3 files Classical, Rapid, and Blitz. These values were modeled on the Classical pgn. To model the coefficients, I first produced some statistics about the dataset. I found the following for Classical-2003-2024-rating2630andUp-NoFRC.pgn:

Code: Select all

Dataset Average Draw Rate: 61.679%
Median RDiff: 34
Median Elo: 2700
White Win: 24.548%
Black Win: 13.773%

I began my coefficient search using two "Penalties." If the formula output for the median rating and median RDiff strayed too far from 61.679% a penalty was added to prevent this. (i.e. Median Elo is 2700, so the formula was fed Ravg=2700 and RDiff=34. 34=Median Rdiff). The second penalty was if two 4200 players were fed into the formula and the draw rate drifted too far from 99.85%.

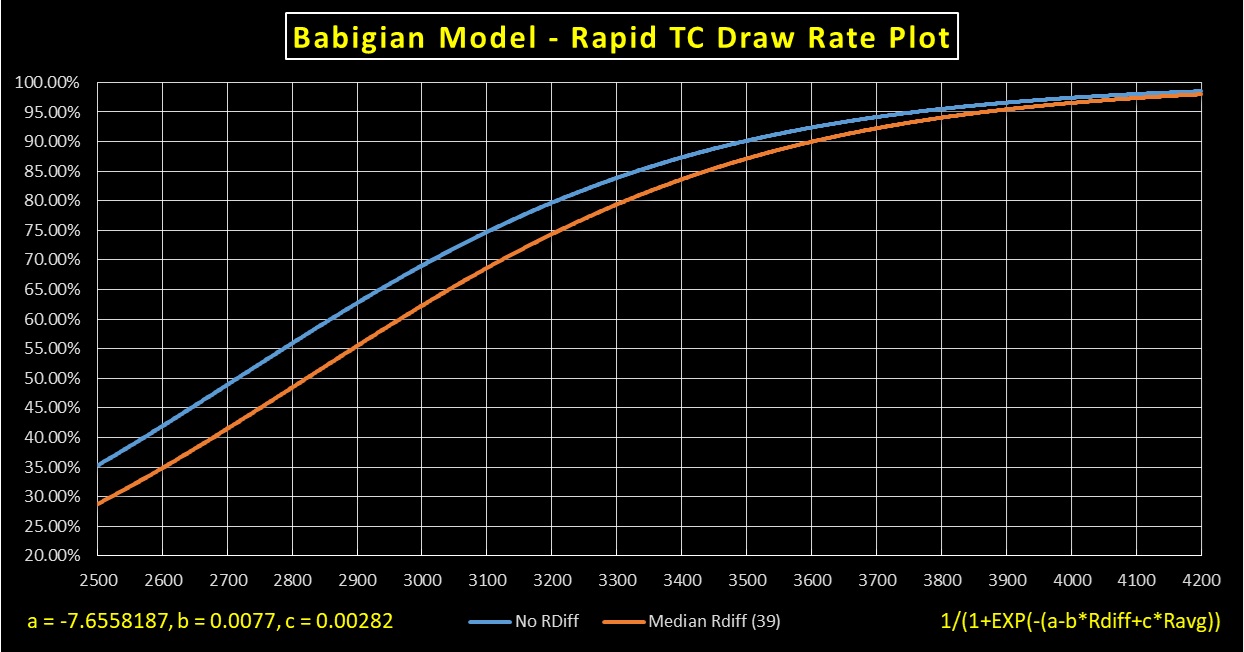
This methodology produced a very reasonable set of coefficients and I've graphed the result using two players of equal strength from 2500 to 4200 and two players centered +-17 Elo around the x axis value (median Rdiff of the dataset).


(software.farseer.org/Software/ClassicalPlot.jpg)

I look forward to feedback or comments on how well you believe this construct functions for elite classical chess.

A note about Davidson (1 / (1 + EXP(-da * (Ravg + db * Rdiff)))) and GlenDavidson (EXP(gda*Ravg)/(1+EXP(gda*Ravg)+EXP(gdb*Rdiff))). I tried a few times to find working coefficients for these models, but both seem to produce irrational draw rate graphs. In addition, no matter how much I tried to model the dataset, when you insert RDiff's approaching zero, the draw rate skyrockets. I therefore gave up on these two models. Perhaps someone has more information on these models that I didn't find.

Finally, I will find coefficients tuned for the Rapid and Blitz pgn files and post those at a later time. It takes a lot of compute to analyze 10s of thousands of games with billions of combinations of coefficients.

Any feedback is most welcome,
Mike

[mbabigian]

Here are the coefficients for Rapid and Blitz

Code: Select all

Rapid
a = -7.6558187
b = 0.0077
c = 0.00282

Blitz
a = -7.4682031
b = 0.0153
c = 0.002617

http://software.farseer.org/Software/RapidPlot.jpg


http://software.farseer.org/Software/BlitzPlot.jpg

It would be interesting if someone can find better fitting figures.