hgm wrote: ↑Sat Jul 03, 2021 12:31 pm
You must decide for yourself which approach conforms best to your measure of simplicity:
1) Putting extra code in Search() to follow the PV from the triangular array in the first branch of the tree, next to probing the TT and using the TT move.
2) Stuffing the PV from the triangular array back into the TT after each search.
3) Using a TT with buckets of 2, and replace the least deep of those.
4) Just require a very large TT and ignore the problem.
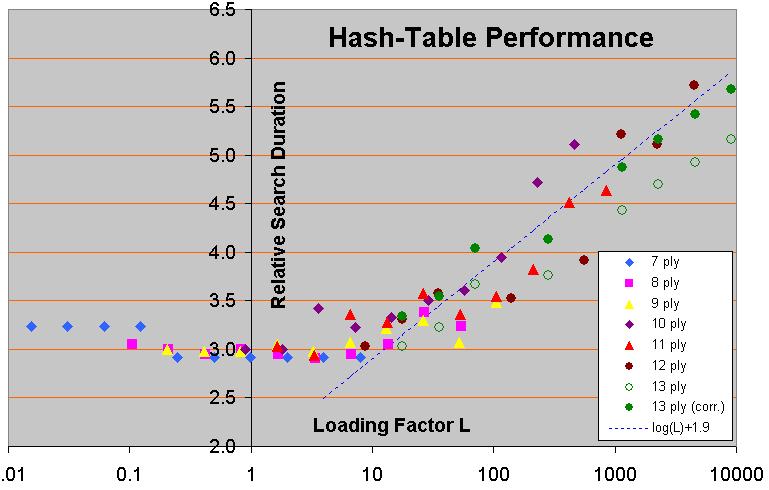
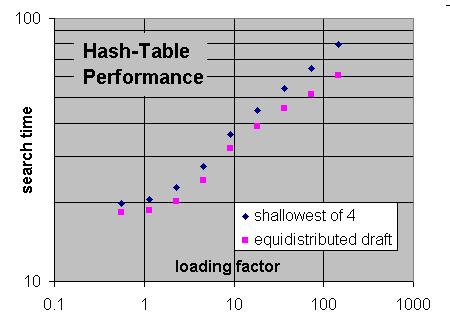
I am biased in favor of (3), as it does not only solve the PV problem in the first branch, but increases the efficiency of the TT through the entire tree. (But, in the limit of very large TT, this advantage of course disappears entirely.) In itself 'shallowest-of-two' replacement is not very complex; it just requires two extra lines of code for manipulating the index to which you map a position:
Code: Select all
index = KEY_TO_INDEX(haskKey);
signature = KEY_TO_SIGNATURE(hashKey); // can, but doesn't have to be entire key
if(TT[index].signature != signature) index ^= 1; // try other entry in 'bucket' if not in first one
if(TT[index].signature == signature) {
// treat hash hit
} else { // hash miss; prepare replacement
if(TT[index].depth > TT[index^1].depth) index ^= 1; // prepare to replace least deep entry in bucket
}
So I have tried solution (2) first where I removed the code that was playing from the PV array directly. Instead the PV of the last iteration is now stored again in the hash before going into Search again to make sure it's available from the TT. Less code and a bit faster, too. In self play against the previous version with 50 MB of hash the ELO gain after 2000 games was +5 ELO (+/- 13) so I reduced the hash size to 5 MB and got +15.1 (+/- 12.8). I also saved a few LOC.
So that is version 0.5.1 now and for 0.5.2 I wanted to test the 2-bucket implementation you suggested where each bucket can also be directly indexed. It was super convenient to add as I just had to change the Index(ulong hash) method really. Extracting the PV from the hash-table recursively is also only a few lines and I can get rid of all tri-table related code. This reduces the LOC from 710 LOC in version 0.5 to 676 LOC. A nice reduction in size.
It also seems to perform really well. There are less position getting kicked out. The tree looks significantly smaller than before, too.
Code: Select all
1. [X] f6f7 g8f7 e1e4 e8e4 f3g5 f7g7 g5e4 d7c6 f1g2 c8e6 f2c2 = +282.00, 4130K nodes, 3605.1517ms
TT Density: 27% TT Overwrites: 8%
2. [X] c6f3 d1f3 h8h2 g2h2 e5f3 h2g2 f3d4 c3b5 e6e5 b5d4 e5d4 = -128.00, 1633K nodes, 1326.4345ms
TT Density: 16% TT Overwrites: 4%
3. [X] b3b5 c6b5 c7c8Q e8f7 c8e6 f7e6 d5c7 e6e7 c7b5 a7a5 b5d4 = +177.00, 2883K nodes, 2742.6361ms
TT Density: 32% TT Overwrites: 9%
4. [X] c8c5 b4c5 d5d3 d2d3 c4c5 g1h1 c5a7 d3d6 a7a4 f1c1 a4e4 = -292.00, 7099K nodes, 5789.4015ms
TT Density: 46% TT Overwrites: 14%
5. [X] c5f2 g1f2 f6g4 f2f1 g4h2 f1g1 c7g3 e2e7 d7e6 e7e8 g8g7 = -154.00, 18798K nodes, 15526.8088ms
TT Density: 83% TT Overwrites: 35%
6. [X] g5f6 d8f6 h6g4 f6f3 g2f3 e5g5 f3e4 g5g4 g1h1 g4e4 b2b4 = +30.00, 5083K nodes, 4296.778ms
TT Density: 35% TT Overwrites: 10%
7. [X] g1g7 f6g7 f5f7 g8h8 c1g1 b7g2 g1g2 e8g8 e5g6 = +615.00, 9733K nodes, 9292.0181ms
TT Density: 53% TT Overwrites: 18%
8. [X] c8g4 f3f2 d5d4 a1e1 d4e3 f1e3 f6d5 d3f1 h3h5 f1c4 g4f3 = -434.00, 9170K nodes, 7894.0597ms
TT Density: 54% TT Overwrites: 18%
9. [X] h5h3 b2b3 h3h8 d2f1 g5g4 f3f4 e5d3 f2e2 e6e5 f1e3 e5f4 = -267.00, 34484K nodes, 28186.6371ms
TT Density: 94% TT Overwrites: 48%
10. [X] g5c1 e1c1 c8c3 c1d2 c3c1 d2c1 d4e2 g1f1 e2c1 b7d5 c1d3 = -64.00, 2246K nodes, 1953.3546ms
TT Density: 22% TT Overwrites: 6%
11. [X] f6g4 f3g4 h8h4 g3f1 b8h8 c4e3 h4h2 f1h2 h8h2 g2f3 = -169.00, 59987K nodes, 45803.6773ms
TT Density: 98% TT Overwrites: 56%
12. [X] c6e7 g8g7 e7g6 h7g6 h4e7 g7g8 e7f8 g8f8 e5g6 f8f7 g6f4 = +332.00, 5736K nodes, 4793.2817ms
TT Density: 41% TT Overwrites: 13%
13. [X] f4d5 e7d5 f3f6 d5f6 c1h6 b7b5 c4d3 f6g4 h6f8 g8f8 e4e5 = +192.00, 6469K nodes, 5740.1143ms
TT Density: 45% TT Overwrites: 14%
If you clear the TT after every move, that is all there is to it, and it is probably simpler and less bug-prone than solution (1). But if you don't clear the TT, the deepest entry in each bucket will eventually get filled with results from deep searches on positions earlier in the game that are no longer reacheable. So that your current search effectively can use only one entry of each bucket. Then you are back in the always-replace situation, but with only half the table size. Therefore people that use such 'depth protection' in their replacement schemes usually combine it with 'aging', where they keep track (in the TT) of whether an entry is used in a search. And if it has not been used for a number of searches, it gets cleared or replaced.
...let's say I want to keep 'age' out of my hash entries to keep them simple...
If you don't want to keep track of aging in the entry, you could erase them 'stochastically' at such a low rate that on average they wil survive for, say, 5 searches. Or just keep track of how many entries of each depth are in the table, and overwrite entries of that depth when there get too many of those.
The positions are randomly placed all over the table so do I really have to randomly delete them? Can't I just delete 1/5th of the table after each searched concludes. That way after 5 searched moves all positions have been cleared exactly once.
...and another idea: After a move was searched to depth X the opponent plays and when it's my turn again two moves have been played. So I can be pretty sure that all positions with depth >= X - 2 are not going to be useful anymore and I could just explicitly purge those. Smaller depth positions might not get purged that way but could get overwritten organically. Would that be enough or would these medium-depth positions still clot up the TT with unreachable positions?