Tata Steel 2025 Simulation Results

[mbabigian]

Below are the round by round simulation results from the draft simulator discussed in this thread viewtopic.php?t=84706.

Assumptions are as follows:
White advantage ~31 Elo. Calculated using a 61% draw rate and a white advantage of 5.7% (figures from analyzing top games database).
Tilt Elo = -20 after two successive losses. Increases by 25% per additional loss.
SB tiebreaks.


http://software.farseer.org/Software/AfterRound6.jpg

The x-axis are round numbers. Round 0 is the simulation probabilities before round 1. Round 1 is after round 1 etc. As you can see, Gukesh really saved his chances by drawing today's lost game against Nordirbek. Fedoseev's chances have also tanked after his loss.

The simulator still needs a lot of work, including knockout pairings for CCT, but it appears to be working reasonably well using the draw rate formula and coefficients mentioned in the other thread.

FYI,
Mike
P.S. Why do images not display here? Just says "Image" where the chart should be.

[Ajedrecista]

Hello Mike:

Congratulations. I also do not know why the image is not displayed here, being a JPG (size of 1447×780). It is true that the link warns my AV with lacking certifications or so.

Focusing on the simulations, I did not expect to see Arjun's chances that low before the start of the event, given his rating. Your 'after round 6' top winning probabilities summarize in Nordibek's almost 40%, Praggna's and Gukesh's circa 25% and Fedoseev's 5% (almost 95% among these four). Let us wait and see.

It seems that your goal is similar to Gambletron 2000 site (not to be confused with Gamble-Tron 2000 'worthless hunk of junk' machine, as seen in action here after evaluating millions of pieces of data in the blink of an eye). In the last Cincinatti vs. Miami game of the NFL, as seen with the disgraceful Gamble-Tron 2000 machine, the graph of the changing probabilities in the correct site looks like this:

https://www.gambletron2000.com/nfl/5544 ... i-dolphins

A bit about their model can be found here.

Regards from Spain.

Ajedrecista.

[mbabigian]

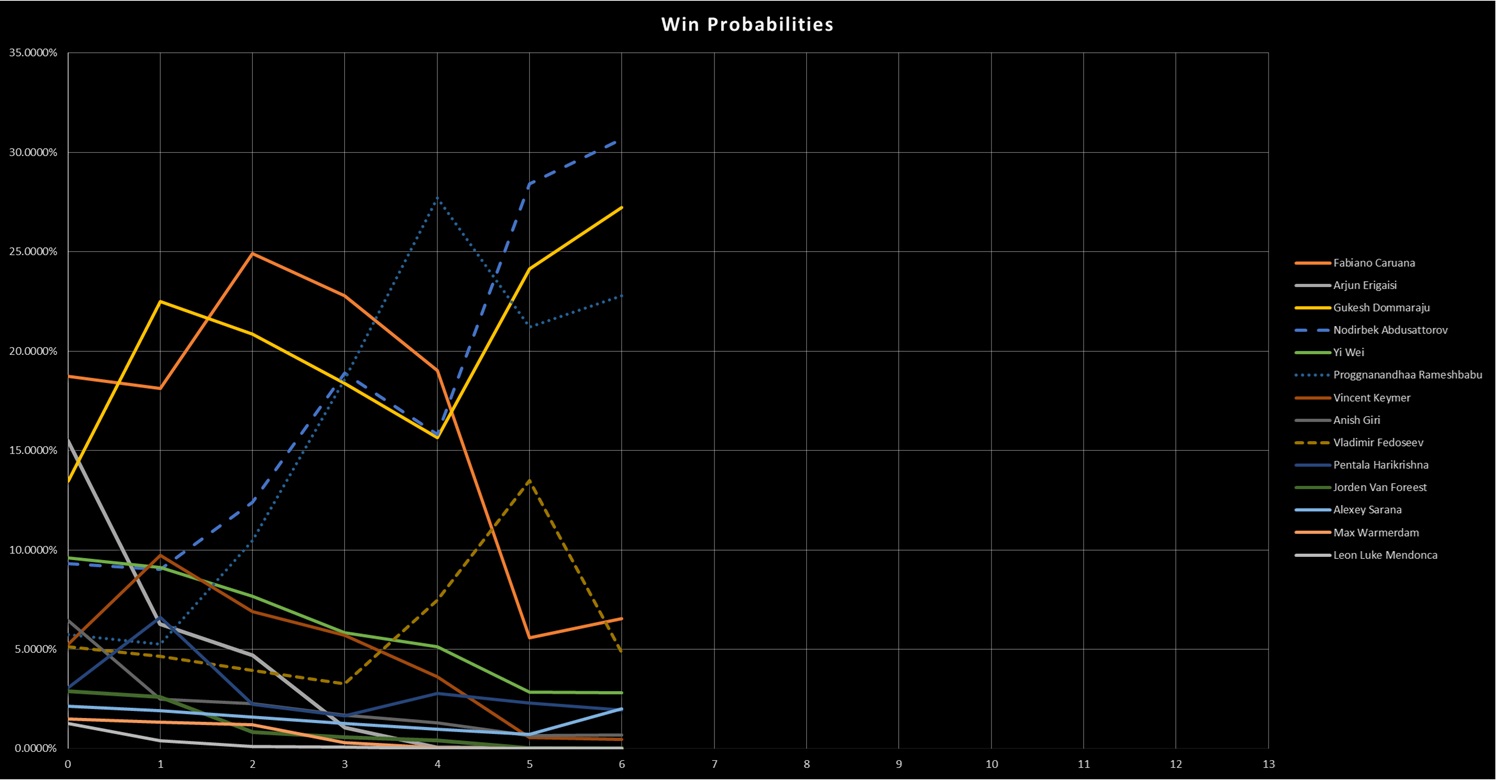
I too was surprised by the round 0 predictions. It appears to be related to who gets white against who. I discovered this by accident. The Tata Steel site did not say the order of the players for pairing.

My program uses the Berger Tables for pairing:

Code: Select all

Rd 1: 1-14, 2-13, 3-12, 4-11, 5-10, 6-9, 7-8.
Rd 2: 14-8, 9-7, 10-6, 11-5, 12-4, 13-3, 1-2.
Rd 3: 2-14, 3-1, 4-13, 5-12, 6-11, 7-10, 8-9.
Rd 4: 14-9, 10-8, 11-7, 12-6, 13-5, 1-4, 2-3.
Rd 5: 3-14, 4-2, 5-1, 6-13, 7-12, 8-11, 9-10.
Rd 6: 14-10, 11-9, 12-8, 13-7, 1-6, 2-5, 3-4.
Rd 7: 4-14, 5-3, 6-2, 7-1, 8-13, 9-12, 10-11.
Rd 8: 14-11, 12-10, 13-9, 1-8, 2-7, 3-6, 4-5.
Rd 9: 5-14, 6-4, 7-3, 8-2, 9-1, 10-13, 11-12.
Rd 10: 14-12, 13-11, 1-10, 2-9. 3-8, 4-7, 5-6.
Rd 11: 6-14, 7-5, 8-4, 9-3, 10-2, 11-1, 12-13.
Rd 12: 14-13, 1-12, 2-11, 3-10, 4-9, 5-8, 6-7.
Rd 13: 7-14, 8-6, 9-5, 10-4, 11-3, 12-2, 13-1.

I assigned all the players that got white in round 1 to 1 through 7 and black players to 8-14, not realizing that the second round pairings would not match unless I knew who was really player 1 or 7 etc. It wasn't until the second round was paired that I could reconstruct the player numbers that Tata Steel used. I then reran, round zero and was startled at what a big difference it made. This difference shows clearly how unfair single round robins really are. I suspect when I code the knockout pairings used at CCT, similar weirdness will appear.

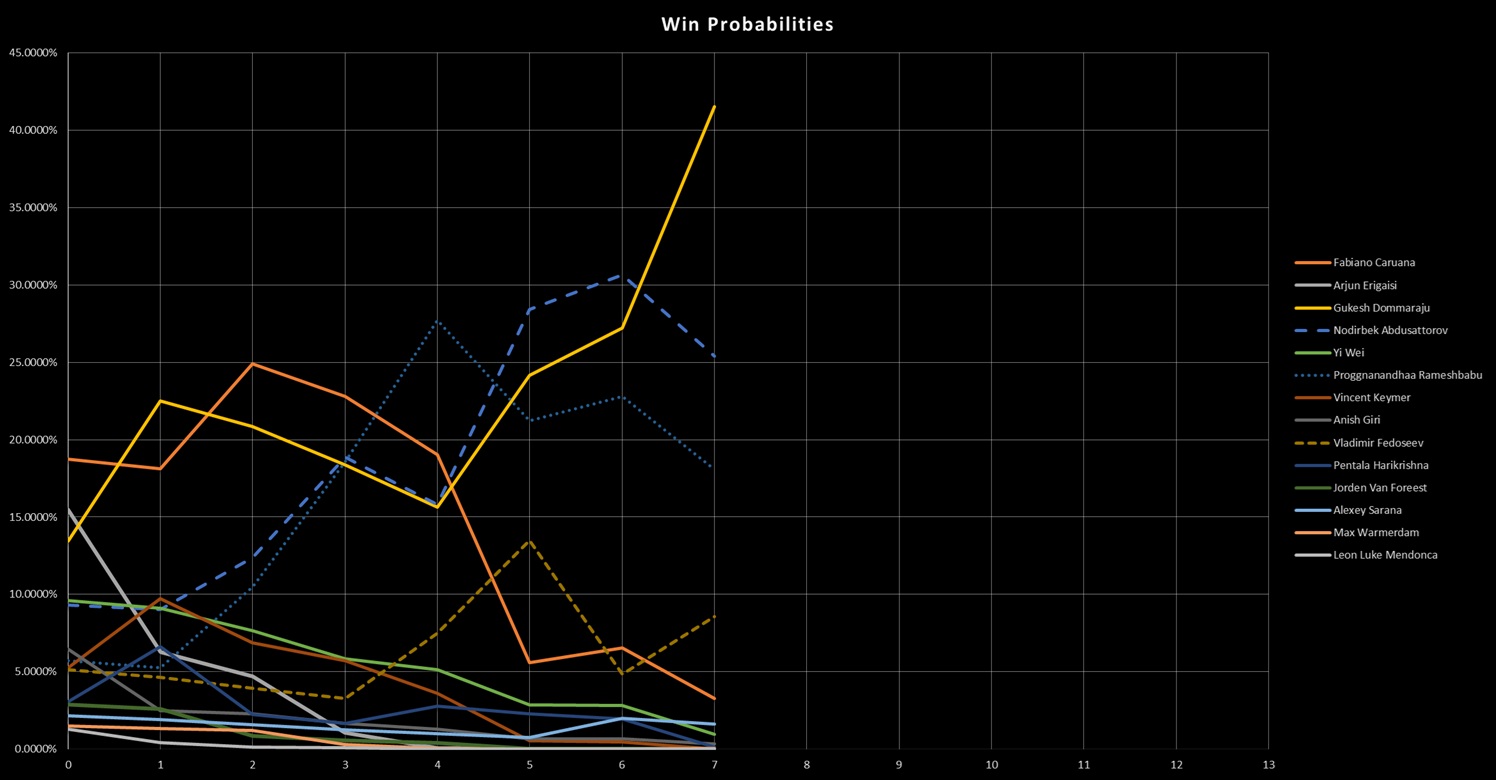
Probabilities after round seven are below.



Thank you for pointing out the browser warning. I never configured SSL certificates for that subdomain so you only use http:// not https:// I decided to install a certificate on that subdomain so that it could be accessed via SSL. I then tried again with this post and I now see the image inline. My browser didn't throw a warning about the domain not having SSL support.

As always, I appreciate your input. It appears it is a three-way race with Fedoseev a distant 4th.
Mike.

[BeyondCritics]

...
Assumptions are as follows:
White advantage ~31 Elo. Calculated using a 61% draw rate and a white advantage of 5.7% (figures from analyzing top games database).
Tilt Elo = -20 after two successive losses. Increases by 25% per additional loss.

I have two problems with that:
You should not simply assume, that a professional plays significantly worse after losses. Assuming independence is the safe bet. E.g. Prof. Rosenthal recently checked allegedly suspicious game streaks of GM Nakamura [1] and in the process tested the time series of his games for auto correlation. He found nothing significant, like his many predecessors.
Also it should be surprising, that white's opening advantage is more or less exactly the same as 30 years ago, since at least for engines any opening advantage has vanished completely, except for the Reti maybe, and professionals normally claim to pick that up. Would you still get an White advantage of 30 Elo points, if for estimating you only consider games from the last 5 years and only from players with Elo 2700 and above?


[1] https://probability.ca/jeff/ftpdir/chessstreaks.pdf

[mbabigian]

Tilt is something I built to experiment with and can be turned on/off, adjust the successive loss count before it is used, as well as the tilt Elo and increase per additional loss if any. I have been experimenting by running with and without it every round. At the current settings there is no significant impact to the results. Only very large tilt values shift the numbers out of the noise with 10,000,000 simulated tournaments.

White's "Elo" advantage varies with the assumed draw rate. Just looking at recent high level matches you can confirm that the advantage is in the 5% range. (Somewhere between 5 & 6). Note, that this is in percent calculated from wins & losses. To get Elo, you have to know the draw rate.

So take this tournament as a tiny example (if you consider it recent ), what is the draw rate? What is White's advantage in percent? Calculate the white Elo advantage, then change the draw rate to 50% and 85%. What was the Elo advantage at these figures?

My simulation calculates the Elo advantage from these two figures and I can change the assumed draw rate and white win percentage before each run. I picked 61% draw rate and 5.7% white advantage because it matched the data. Should tournaments have higher draw rates or lower white win percentages, I can change the figures. If you read the other thread, you'll note I've done analysis for rapid and blitz that shows the reduced draw rate in these formats. In addition, if I disagree with the calculated Elo, I can set it directly.

All simulations have assumptions. I made the assumptions for mine configurable so that I can experiment. I can also guarantee that no matter which assumptions I use, even if I use yours, there will be as many people disagreeing with them as grains of sand on the beach. Fortunately most of the assumptions have a relatively small impact on the results.

YMMV,
Mike

[mbabigian]

Also it should be surprising, that white's opening advantage is more or less exactly the same as 30 years ago, since at least for engines any opening advantage has vanished completely, except for the Reti maybe, and professionals normally claim to pick that up. Would you still get an White advantage of 30 Elo points, if for estimating you only consider games from the last 5 years and only from players with Elo 2700 and above?

I reran my figures on the dataset linked in the draw rate calc thread. The dataset contains elite classical time control games between 2003 and 2023. Here are the results:

Draw rate: 61.68%
White adv: 5.39%
White Elo Adv: 37.63

Anticipating complaints about the dataset date range, I reran the figures only including 2013 and later. Result:

Draw rate: 62.33%
White adv: 5.20%
White Elo Adv: 36.28

The dataset I used can be downloaded from a link in this thread viewtopic.php?t=84706

Humans are not engines
Mike

[Jouni]

Gukesh has been really lucky. In first round he won lost game against Giri. Also got draw from lost game against Abdusattorov.
Gukesh - Giri

[d]7k/pp3p2/7b/3PP3/4b2Q/6PP/Pq3nB1/4R1K1 b - - 0 35

Giri 35. -Qb6?? Human chess . Now 36. Qf6+ 1-0.

[mbabigian]

Agreed. Gukesh got lucky three times. He saved two lost games and the Tata Steel organizers gave him an extra white. The inherent unfairness of single round robin events. He now has the highest probability to win the event.

[mbabigian]

It appears Gukesh got lucky 4 times. When the Tata Steel folks picked Sonneborn-Berger as their tie-break, SB appears to interact with the Berger tables such that Player 7 in the pairing tables is in the most advantageous location of all the players getting an extra white. The least advantageous spot is of course with the players that get an extra black, but the position that interacts in the worst way with the berger tables is position 14 (Arjun Erigaisi). To be clear, in order to avoid ties at the end of simulated tournaments, I used a second tie-break (sum of progressive scores) and that may also tilt things slightly over other possible choices for the secondary tie-break.)

Gukesh needs to buy a lotto ticket. Sorry Erigaisi fans...

Below are the probabilities before round 1 if I set every player's rating to 2800 (equal strength opponents). If every pairing position were equal with equal whites and blacks, all players would have a 7.1429% chance of winning the event. Since the first 7 players have an extra white, you'd expect them to all be above 7.1429% and all players 8-14 would be less than this. I didn't expect the SB tiebreaks to further favor certain positions.

Gukesh Dommaraju 9.0478%
Jorden van Foreest 8.9813%
Yi Wei 8.6591%
Max Warmerdam 8.6211%
Leon Luke Mendonca 8.2271%
Proggnanandhaa Rameshbabu 8.0707%
Pentala Harikrishna 7.8784%
Anish Giri 6.3318%
Vladimir Fedoseev 6.2515%
Alexey Sarana 6.0537%
Fabiano Caruana 5.7793%
Nodirbek Abdusattorov 5.7391%
Vincent Keymer 5.6152%
Arjun Erigaisi 4.7439%

If I flip SoPS as primary and SB as secondary, the order changes within the extra white and extra black groups. I must say I'm learning more than I anticipated when I started fiddling with this program.

[Ajedrecista]

Hello Mike:

[...]

[...] This difference shows clearly how unfair single round robins really are. [...]

[...]

As always, I appreciate your input. [...]

[...] He saved two lost games and the Tata Steel organizers gave him an extra white. The inherent unfairness of single round robin events. [...]

Single round robins can be more fair colourwise: simply take an odd number of players instead of even. With the example of your 14-player Berger tables you can make a 13-player draw, just considering player 14 as a dummy and that dummy's fixed board as a fictional board 0, with the players matched to 14 getting a free day and not awarding any points to them in that round. There will be 13 rounds, but only 12 games per player, getting the same number of white and black for each player after the end of the single round robin:

Code: Select all

        |                        ROUND                        |
PLAYER  |  1   2   3   4   5   6   7   8   9  10  11  12  13  | White Black
   1    |  -   W   B   W   B   W   B   W   B   W   B   W   B  |   6     6
   2    |  W   B   -   W   B   W   B   W   B   W   B   W   B  |   6     6
   3    |  W   B   W   B   -   W   B   W   B   W   B   W   B  |   6     6
   4    |  W   B   W   B   W   B   -   W   B   W   B   W   B  |   6     6
   5    |  W   B   W   B   W   B   W   B   -   W   B   W   B  |   6     6
   6    |  W   B   W   B   W   B   W   B   W   B   -   W   B  |   6     6
   7    |  W   B   W   B   W   B   W   B   W   B   W   B   -  |   6     6
   8    |  B   -   W   B   W   B   W   B   W   B   W   B   W  |   6     6
   9    |  B   W   B   -   W   B   W   B   W   B   W   B   W  |   6     6
  10    |  B   W   B   W   B   -   W   B   W   B   W   B   W  |   6     6
  11    |  B   W   B   W   B   W   B   -   W   B   W   B   W  |   6     6
  12    |  B   W   B   W   B   W   B   W   B   -   W   B   W  |   6     6
  13    |  B   W   B   W   B   W   B   W   B   W   B   -   W  |   6     6

I hope no typos. Some patterns arise, such as -WWWWWWBBBBBB columnwise and the fact that no player gets the same side twice or more in a row, which is very fair. The player with the bye advances 7 in each round, with modular arithmetic, so 1 mod 13 ≡ 1 at round 1, (1 + 7) mod 13 ≡ 8 at round 2, (1 + 7 + 7) mod 13 ≡ 2 at round 3 and so on. I would say that each player will not repeat the same seat in the whole tournament (seat: white on board 1, black on board 1, white on board 2, etc.).

Going a bit further, for a n-player single round robin, with n being odd, compute the n+1 Berger tables (also called Schurig algorithm IIRC), or simply go to FIDE Handbook (FIDE realizes about the same tables to work for n and n+1), then get the n+1 player to be a dummy and this board to be a fictional board 0 (the board of byes), then get -WB patterns as before [(n-1)/2 'W' and (n-1)/2 'B'], with the bye to the player [1 + (r-1)·(n+1)/2] mod n at round r.

This should work to any odd number of players in single round robin tournaments, but it is up to the directors of those tournaments to do so.

Regards from Spain.

Ajedrecista.